Skip to contents

GSoC

GSoC.Rmd
#devtools::install_github("ZeroDawn0D/tRiad")
library(triad)

Introduction

This package has been developed as part of Google Summer of Code 2022, with the help of my mentors Di Cook and Harriet Mason. It calculates the Standard Delaunay Triangulations of a set of 2D points using the Sloan(1987) algorithm.

Link to GitHub repository: ZeroDawn0D/tRiad

There are two ways to use triad:

C++ functions (faster but harder to read and modify)

The DelTri() function creates an object of class triad. This object can be plotted.

    x <- runif(100)
    y <- runif(100)
    o1 <- triad::DelTri(x,y)
    plot(o1, type = 'n')

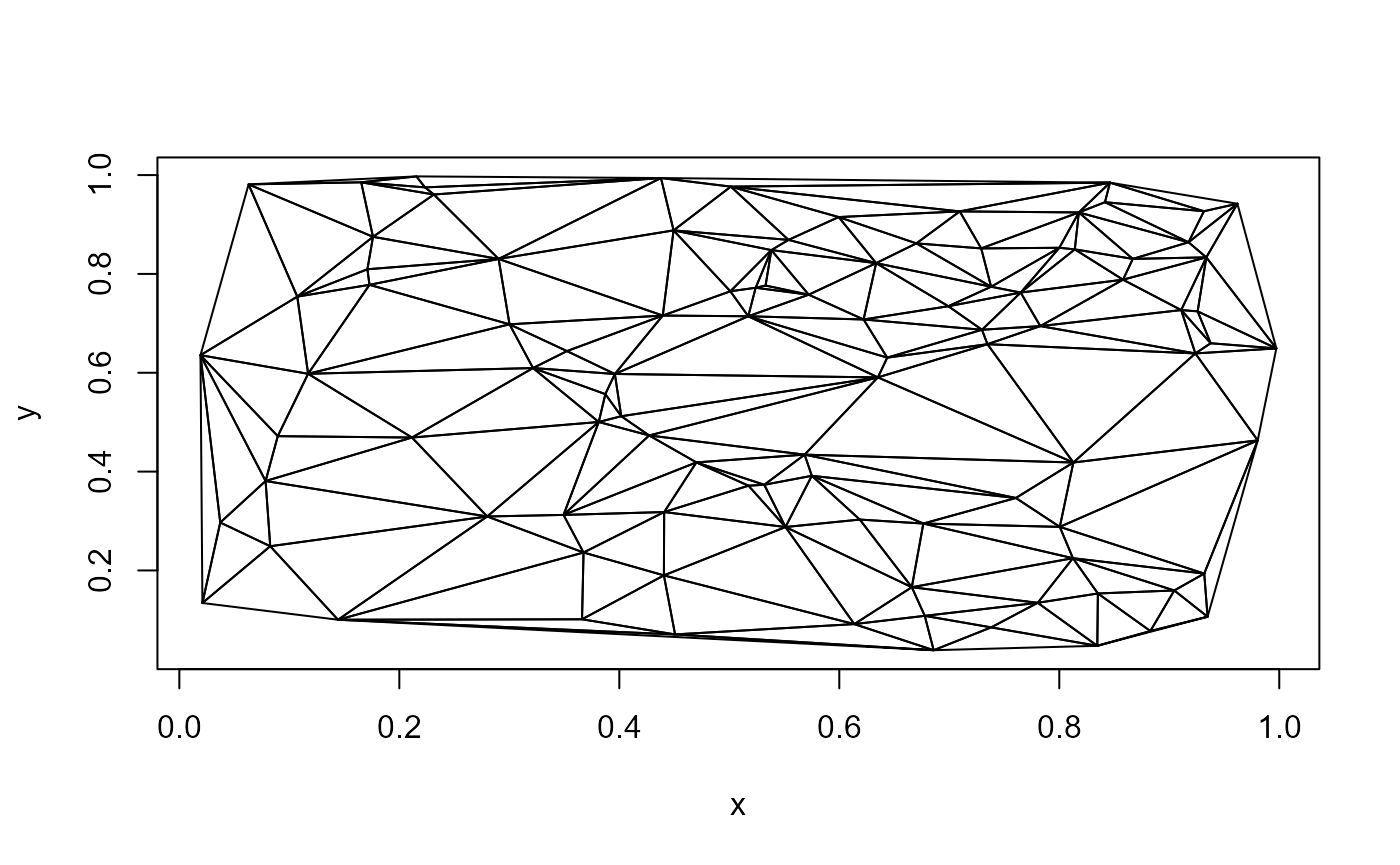
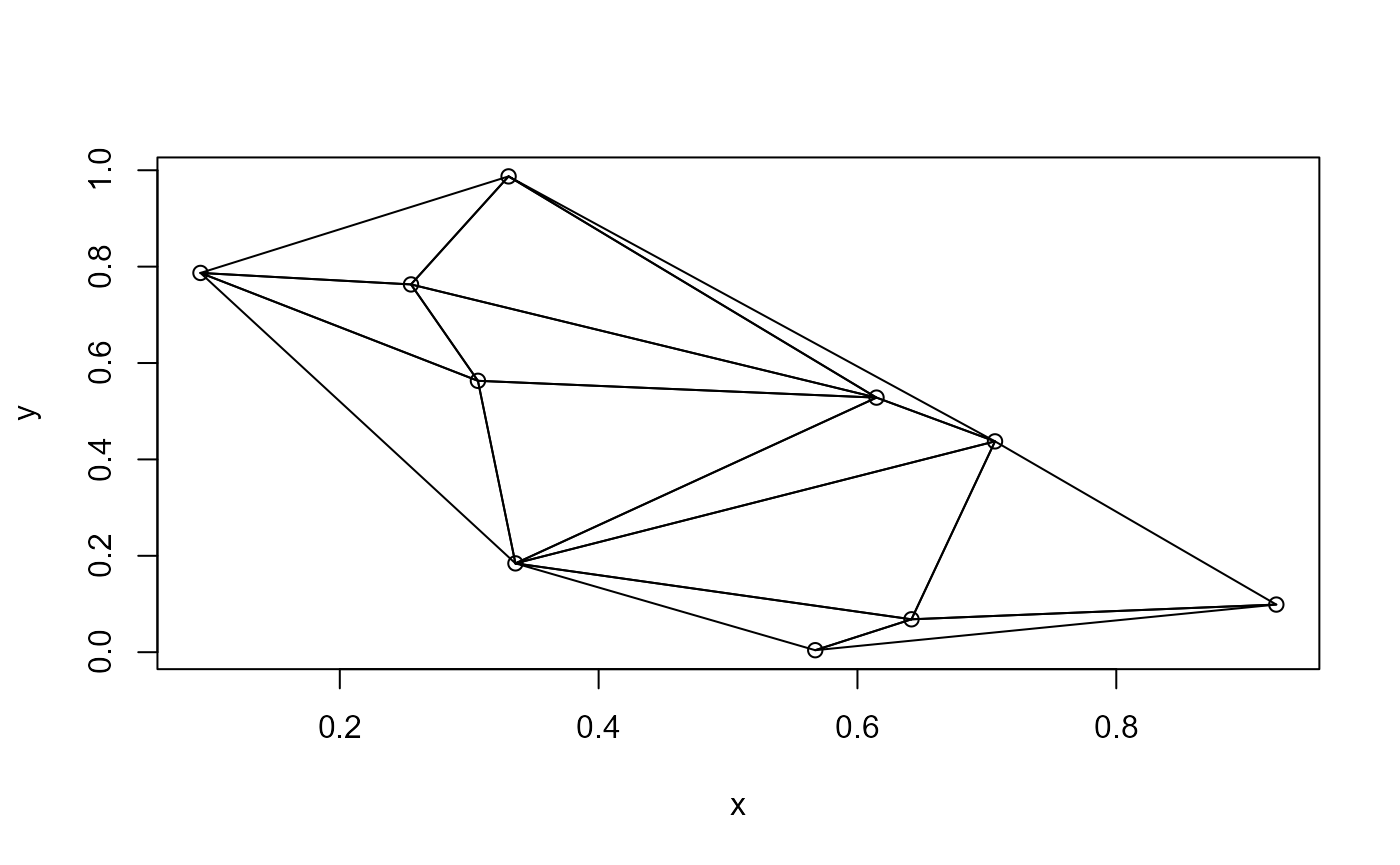
R functions (slower but easier to read and modify)

The del.tri() function does what DelTri() does. The object can be plotted in a similar way.

x <- runif(10)
y <- runif(10)
o2 <- triad::del.tri(x,y)
plot(o2)

Time comparisons

We also compare with interp::tri.mesh()

#install.packages("interp")
library(interp)
#> Warning: package 'interp' was built under R version 4.2.1
x <- runif(500)
y <- runif(500)
system.time(triad::del.tri(x,y))
#>    user  system elapsed 
#>    0.25    0.00    0.25
system.time(triad::DelTri(x,y))
#>    user  system elapsed 
#>    0.02    0.00    0.02
system.time(interp::tri.mesh(x,y))
#>    user  system elapsed 
#>    0.01    0.00    0.02

For larger input:

x <- runif(5000)
y <- runif(5000)
system.time(triad::del.tri(x,y))
#>    user  system elapsed 
#>    6.03    0.89    7.06
system.time(triad::DelTri(x,y))
#>    user  system elapsed 
#>    0.31    0.00    0.31
system.time(interp::tri.mesh(x,y))
#>    user  system elapsed 
#>    0.13    0.00    0.12

SWAP subroutine

The code makes certain changes to the SWAP subroutine. For some reason, the algorithm as described in the paper broke when dealing with concave quadrilaterals.

swapR <- function(x1, y1, x2, y2, x3, y3, xp, yp){
  x1p <- x1 - xp
  y1p <- y1 - yp
  x2p <- x2 - xp
  y2p <- y2 - yp
  dot.1p.2p <- x1p*x2p + y1p*y2p
  mod1p <- sqrt(x1p*x1p + y1p*y1p)
  mod2p <- sqrt(x2p*x2p + y2p*y2p)
  cos.alpha <- dot.1p.2p / (mod1p * mod2p)
  if(cos.alpha > 1){
    cos.alpha <- 1
  }
  if(cos.alpha < -1){
    cos.alpha <- -1
  }
  alpha <- acos(cos.alpha)


  #angle between vector 3->1 and 3->2
  x13 <- x1 - x3
  y13 <- y1 - y3
  x23 <- x2 - x3
  y23 <- y2 - y3
  dot.13.23 <- x13*x23 + y13*y23
  mod13 <- sqrt(x13*x13 + y13*y13)
  mod23 <- sqrt(x23*x23 + y23*y23)
  cos.gamma <- dot.13.23/(mod13*mod23)
  if(cos.gamma > 1){
    cos.gamma <- 1
  }
  if(cos.gamma < -1){
    cos.gamma <- -1
  }
  gamma <- acos(cos.gamma)
  return((alpha+gamma) > pi)
}

Further work

  • Implementing a C++ version of the Constrained Delaunay Triangulations. tripack has a FORTRAN implementation which is not open source
  • plot.triad() is slower than plot.triSh() although both are written in R. Optimise it even further
  • Optimise DelTri() to be as fast as interp::tri.mesh(), if not faster

Optimising C++ code even further

The code makes use of <vector.h> and <stack.h> from the C++ Standard Template Library. Currently, I use vector<vector<double>> to represent 2D matrices, and ample use of push_back(). This leads to a lot of resizing that could slow down the code. I tried to reserve memory beforehand using reserve() but it became even slower. I also tried pre-allocating the memory but it did not work. There could be some way to use double** to optimise it. This is currently a work in progress.